### 集成学习和模型融合Stacking 和Blending方式 参考列表文章１文章２文章３【干货】比赛后期大招之stacking技术分享
前言
- 之前的只是听过，了解大概思想(统计机器学习，最近听闻第二版推出应该好好拜读)，最近准备用它提升一波天池的数据比赛，故而仔细学习。为什么我之前没有刷过这种比赛？因为，１.我之前搞电子选举～民主进步的基石，有空挂上我为了毕业搞的东西～～～。２．没有合适的时间和算力～，这是很烦的～。这个数据比赛，搞个分数容易, 如何刷出较高成绩，着实有些搞头。。。。。。
集成学习
Ensemble learning 中文名叫做集成学习，它并不是一个单独的机器学习算法，而是将很多的机器学习算法结合在一起，我们把组成集成学习的算法叫做“个体学习器”。在集成学习器当中，个体学习器都相同，那么这些个体学习器可以叫做“基学习器”。
个体学习器组合在一起形成的集成学习，常常能够使得泛化性能提高，这对于“弱学习器”的提高尤为明显。弱学习器指的是比随机猜想要好一些的学习器。
在进行集成学习的时候，我们希望我们的基学习器应该是好而不同，这个思想在后面经常体现。 “好”就是说，你的基学习器不能太差，“不同”就是各个学习器尽量有差异。
集成学习有两个分类，一个是个体学习器存在强依赖关系、必须串行生成的序列化方法，以Boosting为代表。另外一种是个体学习器不存在强依赖关系、可同时生成的并行化方法，以Bagging和随机森林（Random Forest）为代表。
附：神经网路的本质，从某个角度讲，是否可以看作深度多层的单logistics模型组成集成学习模型。增加整体的拟合能力，并且融合各个成熟模型的优点和缺点进行查缺补漏
Stacking
一个集成学习框架，两层学习结构，第一层n个不同的分类器，（或者参*数不同,如snapchat理论），合并第一层的输出，作为特征集，并作为下一层的输入。
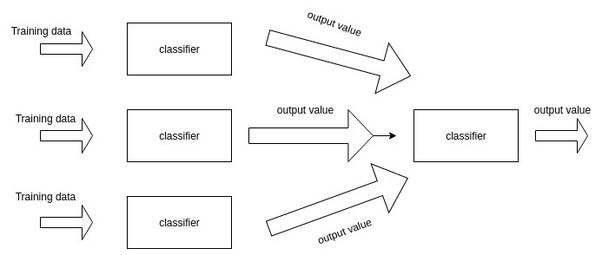引一句知乎的话～
“不同的模型，其实很重要的一点就是在不同的角度去观测我们的数据集。我举个例子，KNN可能更加关注样本点之间的距离关系（包括欧几里得距离（Euclidean Distance）、明可夫斯基距离（Minkowski Distance等等），当样本距离相对较近，KNN就把他们分为一类；而决策树，可能更加关注分裂节点时候的不纯度变化，有点像我们自己找的规则，在满足某个条件且满足某个条件的情况下，决策树把样本分为一类等等。也就是说，不同的算法模型，其实是在不同的数据空间角度和数据结构角度来观测数据，然后再依据它自己的观测，结合自己的算法原理，来建立一个模型，在新的数据集上再进行预测。这样大家就会有个疑问了，俗话说：三人行必有我师。既然是不同的算法对数据有不同的观测，那么我们能不能相互取长补短，我看看你的观测角度，你看看我的观测角度，咱俩结合一下，是不是可以得到一个更加全面更加优秀的结果呢？答案是肯定的。”
同质弱分类器5-folds-validations方法的框架结构与运行过程 bagging
stacking 的思想很好理解，但是在实现时需要注意不能有泄漏（leak）的情况，也就是说对于训练样本中的每一条数据，基模型输出其结果时并不能用这条数据来训练。否则就是用这条数据来训练，同时用这条数据来测试，这样会造成最终预测时的过拟合现象，即经过stacking后在训练集上进行验证时效果很好，但是在测试集上效果很差。
为了解决这个泄漏的问题，需要通过 K-Fold 方法分别输出各部分样本的结果，这里以 5-Fold 为例，具体步骤如下
(1) 将数据划分为 5 部分，每次用其中 1 部分做验证集，其余 4 部分做训练集，则共可训练出 5 个模型 (2) 对于训练集，每次训练出一个模型时，通过该模型对没有用来训练的验证集进行预测，将预测结果作为验证集对应的样本的第二层输入，则依次遍历5次后，每个训练样本都可得到其输出结果作为第二层模型的输入 (3) 对于测试集，每次训练出一个模型时，都用这个模型对其进行预测，则最终测试集的每个样本都会有5个输出结果，对这些结果取平均作为该样本的第二层输入
除此之外，用 stacking 或者说 ensemble 这一类方法时还需要注意以下两点：
1. Base Model 之间的相关性要尽可能的小，从而能够互补模型间的优势
2. Base Model 之间的性能表现不能差距太大，太差的模型会拖后腿
Stacking和Bagging 和 Boosting的区别
组合弱学习器： 为了建立一个集成学习方法，我们首先选择一个待聚合的基础模型。在大多数情况下（包括在众所周知的bagging和boosting方法中），我们会使用单一的基础学习算法，这样一来我们就有了以不同方式训练的同质弱学习器。通过这样同质弱学习器集成得到集成模型，叫做同质集成模型，将异质的弱学习器集成的集成模型为异质集成模型。
集成方法：
自助法、自助聚合（bagging）、随机森林、提升法（boosting）、堆叠法（stacking）以及其他的基础集成学习模型。
最重要的假设是：当弱模型被正确的组合时，我们可以得到更精确和更鲁棒的模型。
在集成学习理论中，我们将弱学习器称为，模型。这些模型可以作为设计更复杂模型的构件。在大多数情况下，这些基本模型本身的性能不是很好，较高的偏置和较高的方差。
集成方法的思想是通过将这些弱学习器，集成模型，从而获得更好的性能。 部分观点引自机器之心 常用的模型集成方法介绍：bagging、boosting、stacking
设计集成方法：最重要的一点，同弱分类器的选择一致。 如果我们选择低偏置高方差的基础模型，我们应该使用一种倾向于减少方差的聚合方法；而如果我们选择具有低方差高偏置的基础模型，我们应该使用一种倾向于减少偏置的聚合方法。
三种元算法：bagging、boostingd、Stacking,
-
bagging , 该方法通常考虑的同质弱学习器，相互独立地并行学习这些弱学习器，并按照某种确定性的平均过程将它们组合起来。（减少的方差，增加泛化性）
-
boosting，该方法通常考虑的也是同质弱学习器，它以一种高度自适应的方法顺序学习这些弱学习器（每个基础模型依赖于前面的模型），并按照某种确定性的策略将它们组合起来。（减少偏置）
-
Stacking，异质弱学习器，并行学习它们，并通过训练元模型集成。
bagging和Boosting Bagging 即套袋法： 1、从原始样本集中，自主法(Bootstraping)的方法抽取n个训练样本。进行K轮，K个训练集K个训练集之间相互独立。 2、每次使用一个训练集，训练一个模型，K个模型。 3、对分类问题：将上步得到的K个模型采用投票方式得到分类结果；回归结果，计算均值作为最后的结果。 百度百科 Boosting： Boosting和bagging、随机森林不同的是个体学习器之间的是否存在强依赖关系，Boosting存在强依赖关系，必须串行生成。后两者不存在可以并行。 1. AdaBoost算法，每次使用的是全部样本，每轮训练改变样本权重。（错误样本权重加大，正确样本权重减小）下一轮训练的目标是找到一个函数f来拟合上一轮的残差。当残差足够小或者设置的最大迭代次数停止后。 2. 残差树， 回归问题，基于CART算法的回归树，加法模型、损失函数为平方函数、学习算法为前向分步算法。 加法模型如下： \(f_M(x) = \sum _{m=1}^{M} T(x;\theta_m)\) 什么叫做残差和前向分步，例子如下，比如小明的年龄是10岁，第一次我们的残差树拟合的值为6，那么第二次我们拟合的目标值为10-6=4。 ～ 3. GBDT算法，其基本原理和残差树类似，基学习器是基于CART算法的回归树，模型依旧为加法模型、学习算法为前向分步算法。不同的是，GDBT没有规定损失函数的类型，向加法算法的每一步都是拟合损失函数。
接着框架方面，AdaBoost(类，基本模型很广泛)—>GBDT(对象，限制在决策树，分类ID和C4.3和回归：CART回归树)和XGBOOST(框架实现)、LightGBM（改进框架）。
关于决策树和GBDT以及XGboost、LightGBM中的决策树的～～需要仔细探究。